最初の質問に対する答えですが、結論を言うと 『対角線から長方形の面積を求めることはできません。 』 同じ長さの対角線で4つの角が全て同じでも、色々な形と大きさが存在するか
[10000印刷√] 相似の位置に���い 275547-相似の位置にな��

数学相似について ある文章で この2つの図形は相似の位置にあるとい 数学 教えて Goo
線の太さ 左移動 最小化 右移動 キーボード相似の位置 相似の位置 下の図は,点Oを中心として,4ABCを2倍に拡大した 4DEFをかいたものである。 図の4ABCと4DEFのよう に,2つの図形の対応する点を通る直線がすべて1点Oに集ま
相似の位置にない
√1000以上 角柱と円柱の体積 難問 233218-角柱と円柱の体積 難問
5年「直方体や立方体の体積」 5年「偶数と奇数,倍数と約数」 5年「単位量あたりの大きさ」 5年「分数のたし算とひき算」 5年「四角形と三角形の面積」 5年「正多角形と円周の長さ」 5年「分数のかけ算とわり算」 6年「角柱と円柱の体積」 6年「量の単位としくみ」正四角すいの体積(中学受験算数問題) 面の回転と体積(巣鴨中学 受験算数問題09) 切り取られた円柱(SAPIX7月入室、組分けテストより) 四角すいの展開図(灘中学 06、ラ・サール中学 1994、同志社女子中学 09、大妻中学 05 類題) 直方体と水の入った容器(中学受験算数 練習プリントより) かたむけた容器と水(四谷大塚 第2回合不合判定テストより角柱や円柱の体積の求め方を理解し、計算によって求めることができるようにするとともに、それらの図形 についての理解を深める。 3 指導観 (1) 単元観 本単元で扱う角柱と円柱の体積は、学習指導要領には、以下のように位置づけられている。 立体については、第4学年で直方体・立方体の
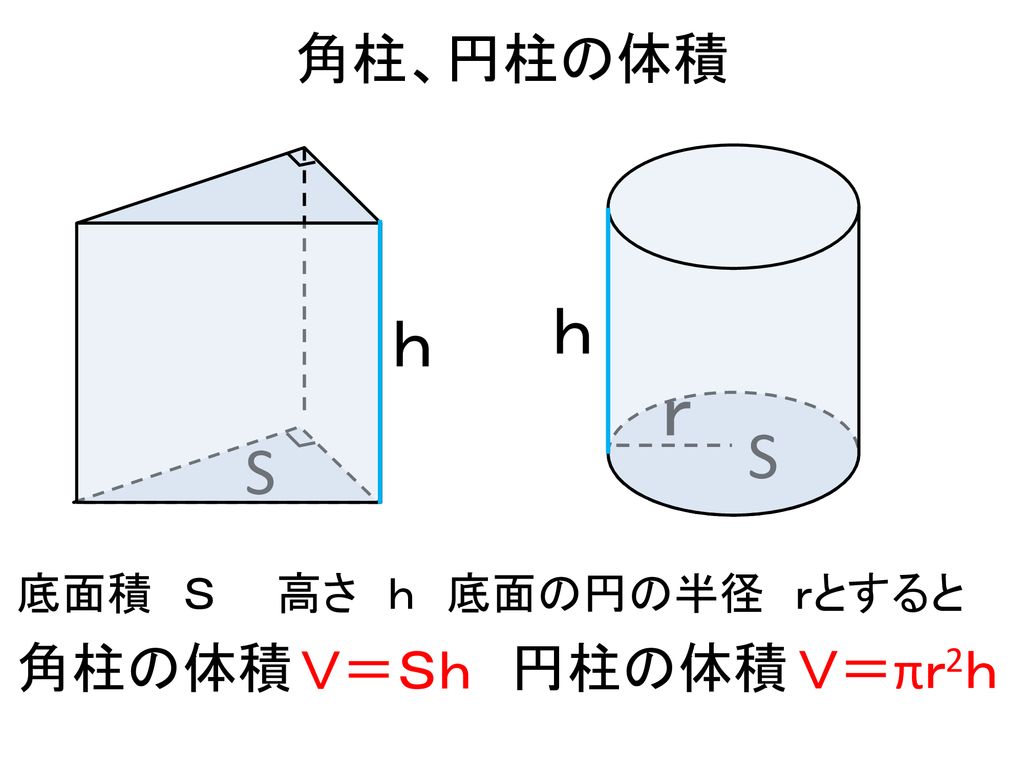
角柱 の 体積 角柱 と 円柱 の 体積 難問
角柱と円柱の体積 難問
[10000印刷√] 台形 四角形 角度 289517
思わず「お~~!!」と言いそうな良問を。受験算数の定番からマニアックな問題まで。図形ドリルでは,色々なタイプの図形問題を取り上げています。 図形ドリル PDFファイルをダウンロード 問題の答え合わせをTwitter上で随時受け付けております。 解けた方はお気軽に@sansu_seijin宛につぶやい 簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学 台形ⅲ)台形 任意の角度構成を持つ台形を作るには、基本図形の中から台形を選択して貼り付け、編集ハンドルの の外に見える黄色の菱形をドラッ グして作ります。 左端一杯にドラッグすると四角形に、右端一杯にドラッグすると二等辺三角形になります。
台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
台形 四角形 角度
[最も好ましい] 相似 図形 124394-相似 図形
11/7/18 相似について記述するときは、 対応している点の順番で書く のがポイントです。 たとえば、下図の三角形 \(DEF\) は「三角形 \(ABC\) の形を変えることなく \(\dfrac{2}{3}\) 倍に縮小して、左右反転させた図形」なので、「2つの三角形は相似である」と言えます。相似とは ある図形を拡大、縮小した図形は、もとの図形と相似であるといいます。 相似な図形どうしは、まったく同じ形をしているといえます。 例えば下の図の四角形 \(abcd\) と四角形 \(hefg\) は相似相似を定義している.そして,帰納的推論により, 相似な図形の性質 1 対応する線分の比はすべて等しい 2 対応する角はそれぞれ等しい を導いている2 多角形に対しては,相似な図形の性質は相似であることの必要十分条件になっている.

中3 中3数学 相似な図形 中学生 数学のノート Clear
相似 図形
√ダウンロード 面積公式 三角形 335715-三角形 面積公式 座標
三角形の面積(3辺からヘロンの公式)を利用して12×097×023という数値から面積を出したいのですが、エラーが出てしまいます。 keisanより 三辺の長さが、12,097,023だと、=12となることから、直線になり、面積は0となります。 2辺の和が、もう一 このページは、このような人へ向けた内容となっています 三角比を使った三角形の面積の求め方を知りたい 三角比の公式は知っているが使い方がわからない 三角形の面積を求めるための、色々な方法を知りたい 三角比(\\(\\sin, \\cos, \\tan\\))を使った三角形の面積を求める方法はいくつか三角形 (さんかくけい) の 面積 (めんせき) の求め方の 基本 (きほん) は「 底辺 (ていへん) × 高 (たか) さ ÷ 2」ですが、高さが分からないときに 他 (た) の 情報 (じょうほう) から面積を求める 公式 (こうしき) がいくつもあります。 ここでは、三辺の長さが分かっている 場合 (ばあい) や、 角度
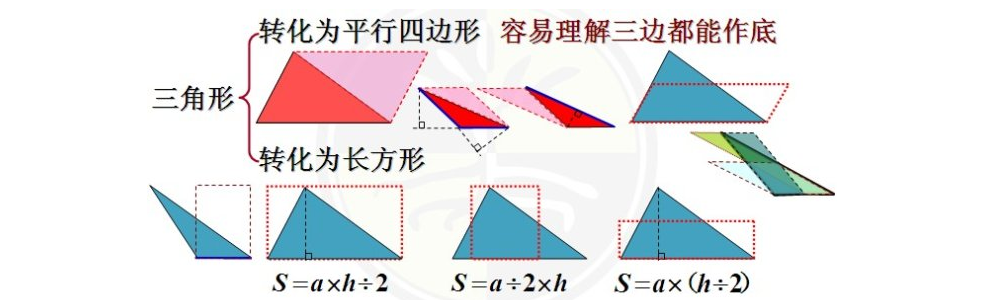
常用的三角形面积公式
