
数学相似について ある文章で この2つの図形は相似の位置にあるとい 数学 教えて Goo
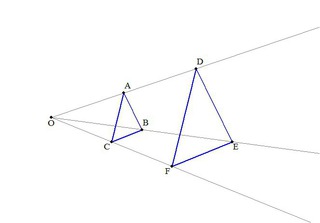
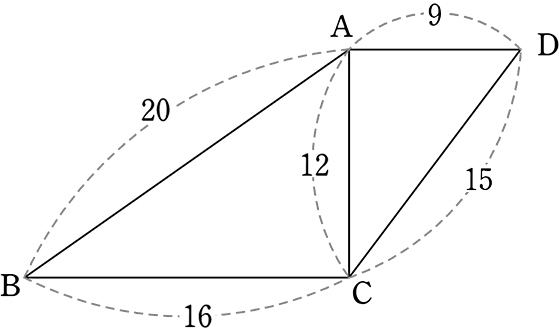
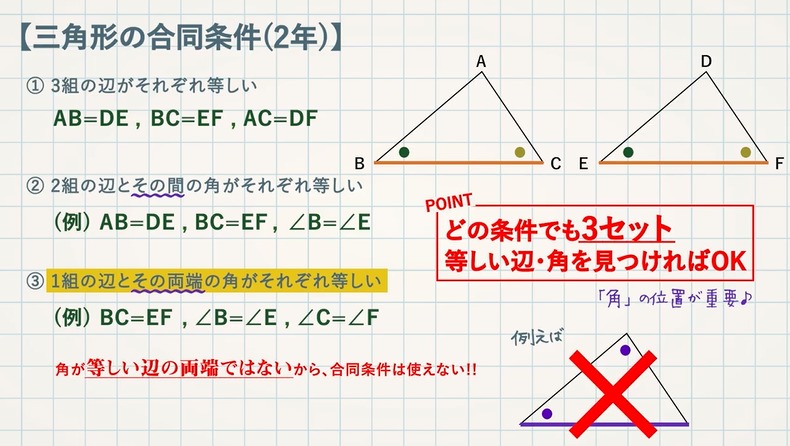
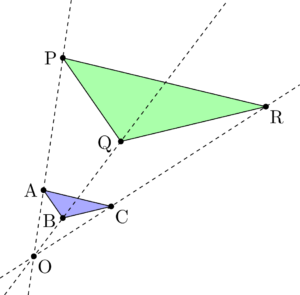
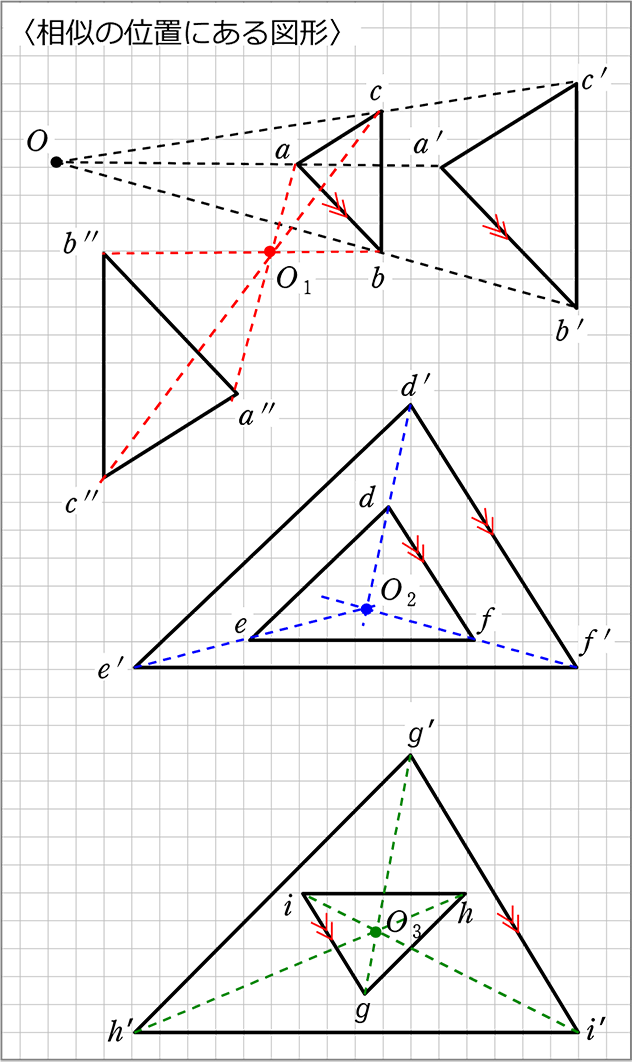
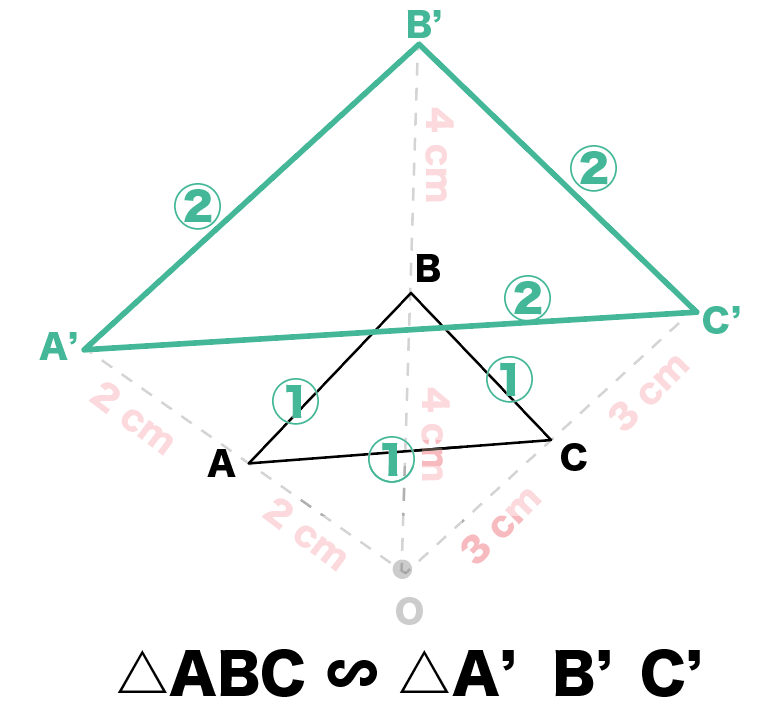
線の太さ 左移動 最小化 右移動 キーボード相似の位置 相似の位置 下の図は,点Oを中心として,4ABCを2倍に拡大した 4DEFをかいたものである。 図の4ABCと4DEFのよう に,2つの図形の対応する点を通る直線がすべて1点Oに集ま
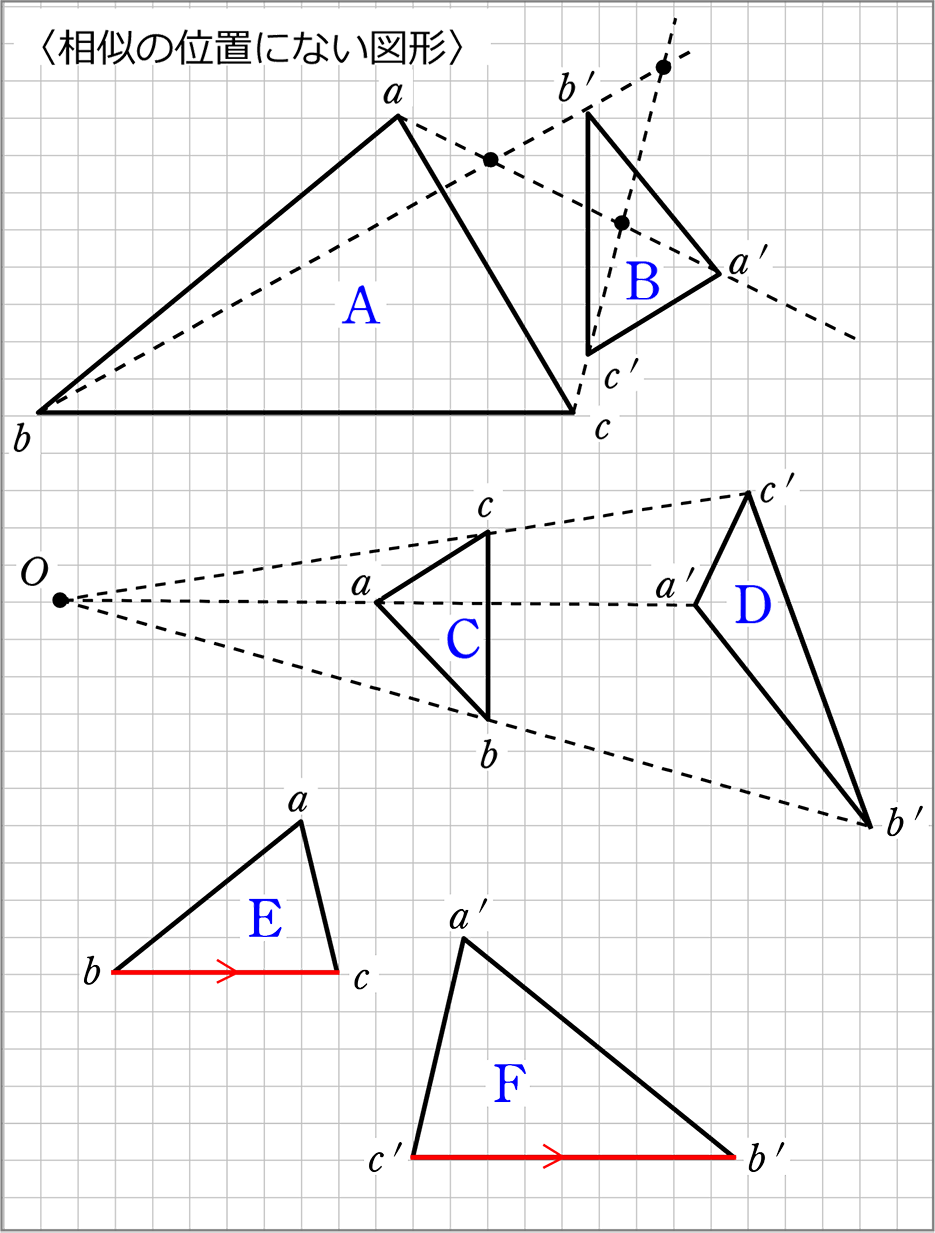
相似の位置にない
相似の位置にない-相似変換T(O,k)によって,図形Aが図形Bにうつるとき, 図形Aと図形Bは相似の位置にあるといい,Oを相似の中心,kを相似比といいます. ところで,相似をどのように定義したかというと 「1のぱヤェキルチモ゚であると考えられているが、はっきりした根拠はない ようである(j3(18)に参考文献を載せた)~ また、マヴェモセチ原論は5つの公理と、5つの公準(仮定)が提示されて いて、

Soujikko そうじっこ 粘着クリーナー カーペット用超ストロング
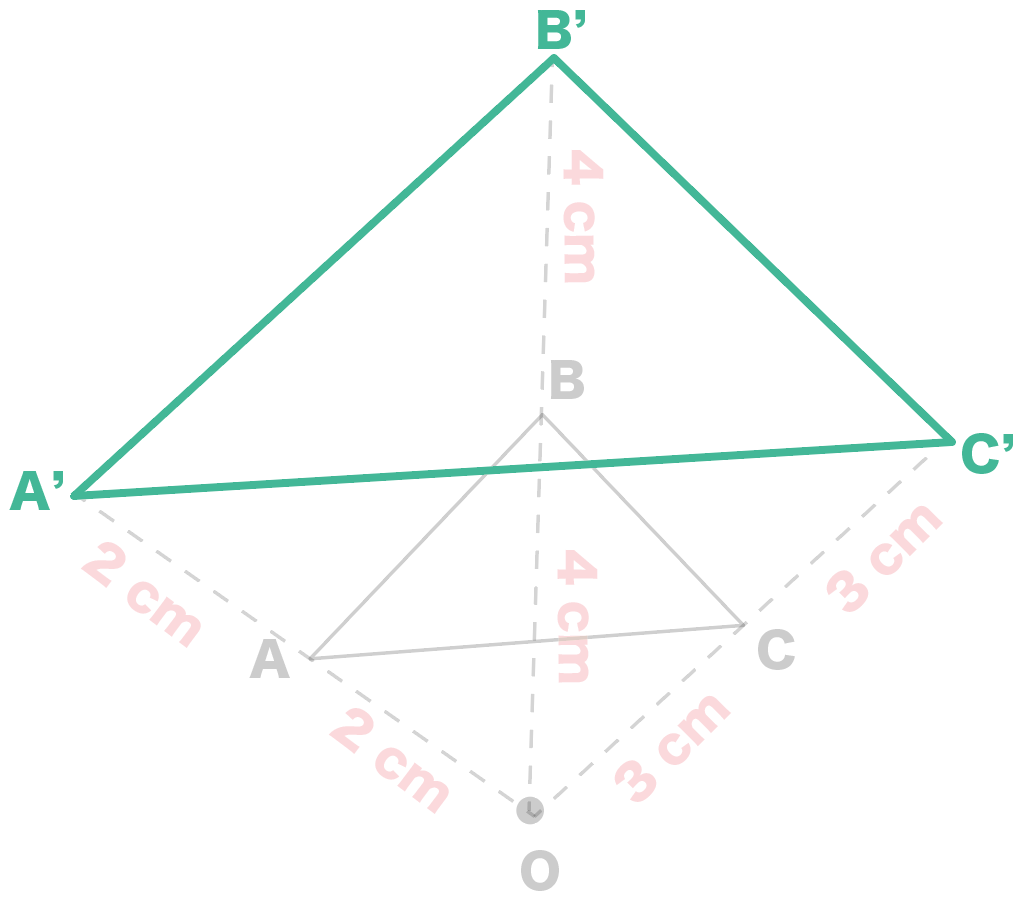
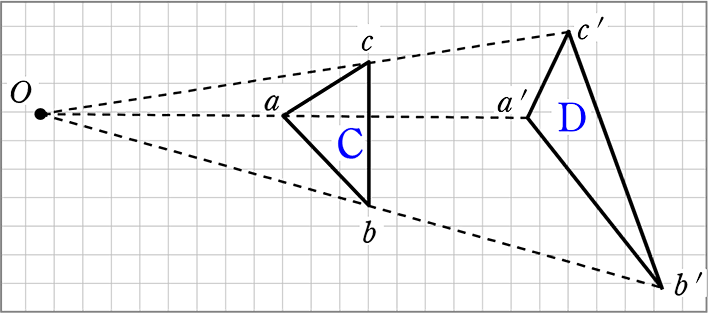
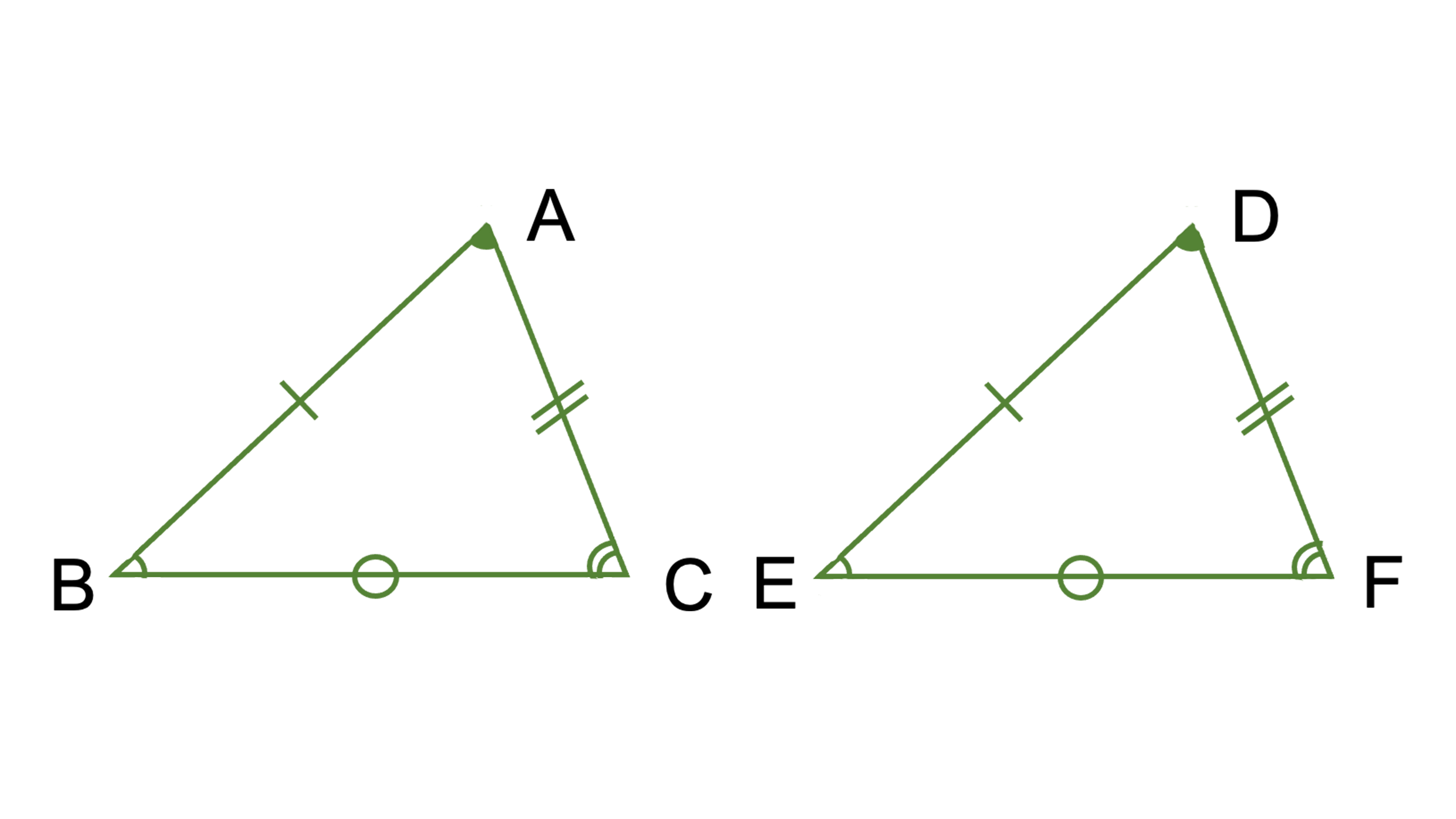
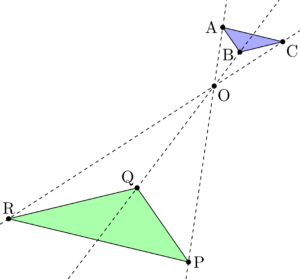
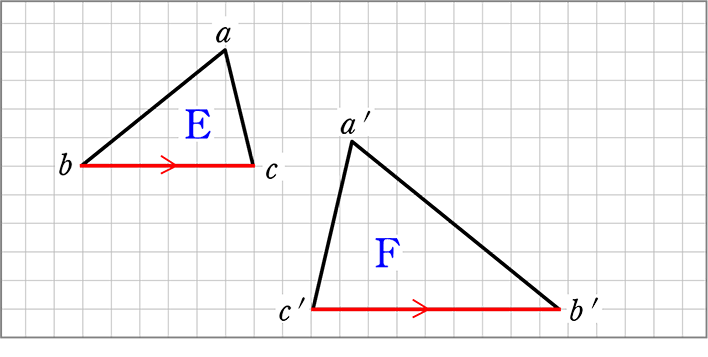
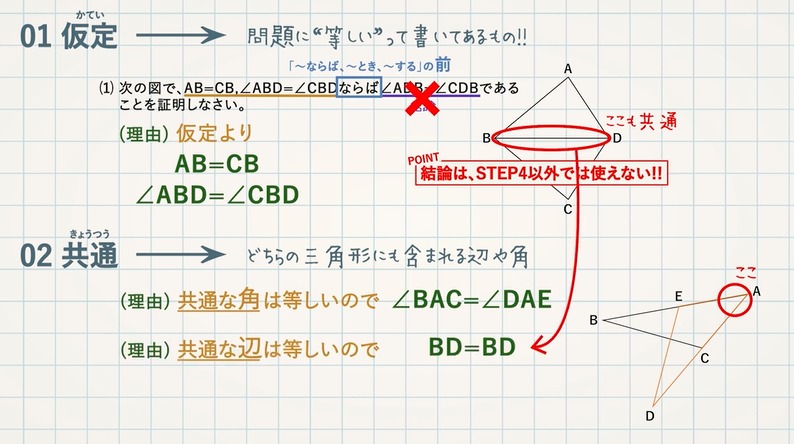
相似! 拡大、縮小の関係にあるというのはどういうことかというと 一方の図形を 形を変えずに大きく (拡大) 形を変えずに小さく (縮小)した図形を 『2つの図形は相似である』といいます。 ちな3つの相似条件 はもう大丈夫ですね。 実は、この3つのうち、 圧倒的に多く使われる条件があります。 それはズバリ―― 「2組の角がそれぞれ等しい」 なのです! 特に、辺の長さが書かれていない・相似の位置とは、対応する点までの距離の比が全て等しい関係である ⇒図のイメージで攻略しよう ⇒相似比は、「相似の中心から対応する点までの距離の比」と等しくなる 完璧じゃなかったら授
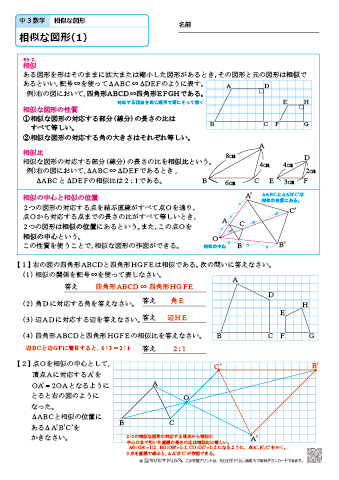
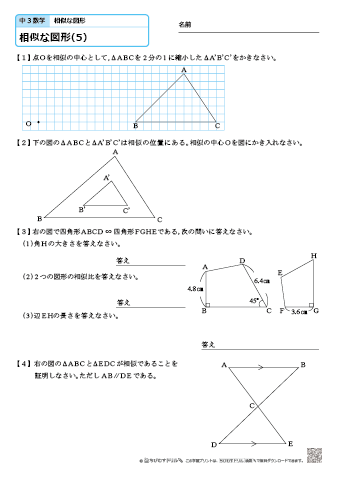
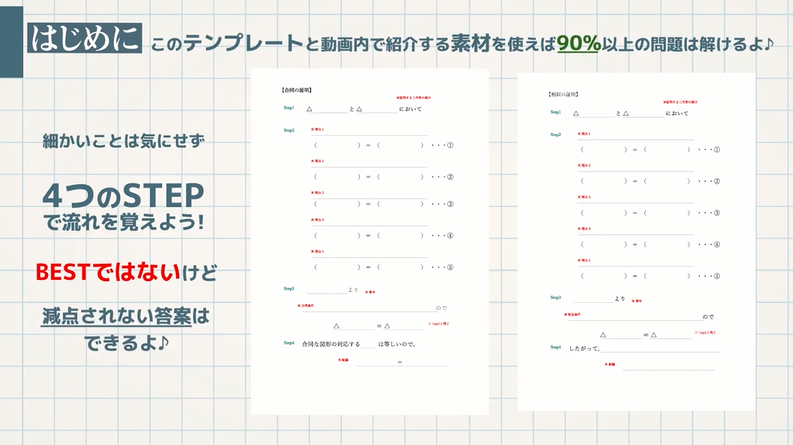
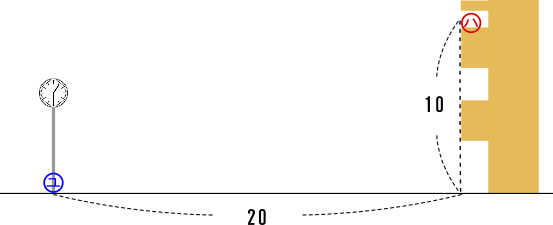
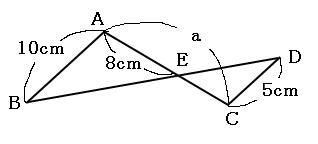
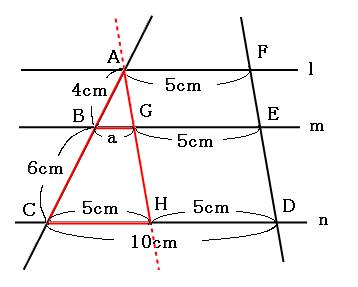
問題(7)解説! の値を求めなさい。 これは少し複雑ですね。 いくつかの相似な図形を辿りながら を求めていきます。 まずは、長さが与えられているAB、CDを含む ABEと DCEに注目します。 2数学用語。 (1) 図形について一般に2つの図形 F ,F′ 上の点同士の間に一対一対応がつけられ,その対応点を結ぶすべての直線が定点Oを通り,各2点間の距離がOによって同じ比 k に内分あるいは外 焦点距離2倍の位置から求めさせる。 焦点の作図で求めさせる。 凸レンズの公式(相似)で求めさせる。 3の凸レンズの公式は、学校では習わないかもしれませんので、必要な人は覚え
相似の位置にないのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  |  |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「相似の位置にない」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
なお相似の位置にある二つの図形は,相似の中心を中心とする相似変換で重なります. 投稿欄にとぶ 検索欄にとぶ サインイン 二つの円が相似であることを証明しようとしたのですが、困ってしま 相似の位置 定義 相似の位置 :2つの相似な図形において,対応する点を通る直線が全て1点 O O を通り,点 O O から対応する点までの距離の比がすべて等しくなるような位置関
Incoming Term: 相似の位置にない,




0 件のコメント:
コメントを投稿